Navigation▲
| Tutoriel précédent : Pilotage par le logiciel | Sommaire | Tutoriel suivant : Rasterization |
II. Introduction▲
Nous allons maintenant voir les circuits chargés de gérer la géométrie. Il en existe deux grands types :
- l'assembleur d'entrées ;
- et les circuits de traitement de sommets.
III. Assembleur d'entrées▲
Avant leur traitement, les sommets à traiter sont stockés dans un gros tableau en mémoire vidéo. Ce gros tableau s'appelle le tampon de sommets. L'assembleur d'entrées (input assembler) est un circuit qui va charger les sommets de la mémoire vidéo dans notre pipeline de rendu, vers les unités de traitement des sommets.
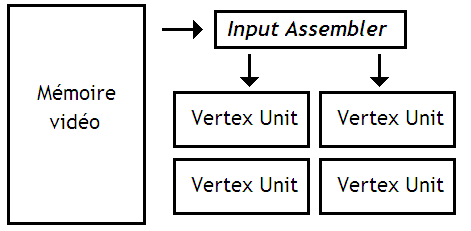
Pour ce faire, il a besoin qu'on lui dise où est ce tableau dans la mémoire : son adresse de départ. Il a aussi besoin de la taille du tableau. Ensuite, il faut qu'on lui dise de quels types sont les données qu'on lui envoie : les sommets sont-ils codés sur 32 bits, 64, 128, etc. Il faut dire que suivant les jeux, les sommets ne font pas forcément la même taille. Pour cela, cet assembleur d'entrées dispose de registres, qui stockent l'adresse de départ du tableau, sa taille, et les informations sur les sommets. En fonction du contenu de ces registres, il calcule l'adresse des sommets à charger, envoie l'adresse à la mémoire vidéo et récupère le résultat.
L'assembleur d'entrées peut aussi gérer des lectures simultanées dans plusieurs tampons de sommets. Généralement, la mémoire vidéo permet d'effectuer plusieurs accès simultanés facilitant la tâche de l'assembleur d'entrées.
III-A. Triangle en bande▲
Il arrive souvent qu'un sommet soit réutilisé dans plusieurs triangles ou primitives. Par exemple, prenez un simple cube.
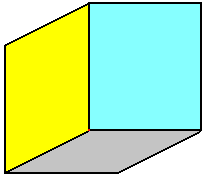
Le sommet rouge du cube appartient aux trois faces grise, jaune et bleue. Le sommet sera donc présent en trois exemplaires dans le tampon de sommets. Un exemplaire pour la face bleue, un pour la jaune et un pour la grise. La consommation de mémoire vidéo sera alors assez importante.
Pour éviter ce gâchis, les concepteurs des bibliothèques et de cartes graphiques ont inventé des techniques pour limiter la consommation de mémoire. La première de ces techniques est celle des triangles en bande (triangle strip). Elle permet d'optimiser le rendu d'un objet constitué de triangles placés en série, les uns à la suite des autres. Les triangles placés sur un objet de ce genre sont collés les uns contre les autres. Ils ont une arête et deux sommets en commun.
Dans ces conditions, une optimisation possible consiste à ne pas stocker en double les deux arêtes communes à un triangle. Avec cette technique, seul le premier triangle, le plus à gauche, est stocké intégralement en mémoire. Les autres triangles sont simplement codés avec un seul sommet. Ce sommet sera alors combiné avec les deux derniers sommets chargés par l'assembleur d'entrées pour former un nouveau triangle.
En mémoire, le gain est énorme : au lieu de trois sommets pour chaque triangle, on se retrouve avec un sommet pour chaque triangle, sauf le premier de la surface. Le gain en mémoire est proche de trois.
L'assembleur d'entrées gère ces triangles nativement sur les cartes graphiques pas trop anciennes. Pour gérer ces triangles en bande, l'assembleur d'entrées doit conserver les deux derniers sommets utilisés, afin de pouvoir rendre le triangle comme il faut. Pour cela, il incorpore une petite mémoire capable de stocker deux sommets.
III-B. Triangle en éventail▲
Une autre forme de stockage optimisée des triangles existe : les triangles en éventail (triangle fan). Cette technique fonctionne comme pour les triangles en bande : chaque triangle est stocké sous la forme d'un unique sommet, qui est combiné avec les sommets précédents pour former un triangle.
Sauf que cette fois-ci, le sommet n'est pas combiné avec les deux sommets précédents. Pour comprendre le principe, nous allons utiliser un exemple. Supposons que je crée un premier triangle. Celui-ci contiendra trois sommets : v1, v2, v3, qu'on chargera dans cet ordre. Ensuite, je vais charger le sommet v4, pour créer un nouveau triangle. Avec la technique des triangles en bande, les deux sommets réutilisés auraient été les sommets v2 et v3. Avec les triangles en éventail, les sommets réutilisés sont les sommets v1 et v3.
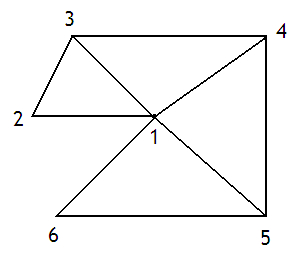
Ces triangles en éventail sont utiles pour créer des figures comme des cercles, des halos de lumière, etc.
III-C. Tampon d'indices▲
Enfin, nous arrivons à la dernière technique. Avec celle-ci, chaque sommet sera stocké en un seul exemplaire dans le tampon de sommets. Ce tampon de sommets est couplé à un tampon d'indices : un tableau qui va servir à stocker des indices. Ces indices sont des nombres ou des adresses mémoires, qui servent à localiser le sommet voulu dans le tampon de sommets. Quand on voudra charger un sommet depuis la mémoire vidéo, il suffira de fournir l'indice du sommet : l'assembleur d'entrées chargera alors le sommet voulu depuis la mémoire. Pour charger plusieurs fois le même sommet, il suffira de fournir le même indice à l'assembleur d'entrées.
Dit comme cela, on ne voit pas vraiment où se trouve le gain en mémoire. On se retrouve avec deux tableaux : un pour les indices, un pour les sommets. Le truc, c'est qu'un indice prend beaucoup moins de place qu'un sommet.
Un indice tient au grand maximum sur 32 bits, là où un sommet peut prendre 128 à 256 bits facilement. Entre copier sept fois le même sommet, et avoir sept indices et un sommet, le gain en mémoire est du côté de la solution à base d'index. Quand on sait qu'un sommet est souvent réutilisé entre quatre et six fois…
III-D. Cache de sommets▲
Sans tampon d'indices, chaque sommet chargé depuis la mémoire l'est une seule et unique fois. Avec la technique du tampon d'indices, un même sommet peut être chargé plusieurs fois depuis la mémoire vidéo. Cela peut paraître anodin, mais cela permet d'utiliser des optimisations assez intéressantes.
L'accès à la mémoire vidéo est très lent. C'est un peu le problème avec les mémoires : plus elles sont grosses, plus elles sont lentes. Pour limiter la casse, les cartes graphiques intercalent une petite mémoire ultrarapide entre la mémoire vidéo et la sortie de l'input assembler. Cette mémoire s'appelle le cache de sommets (vertex cache).
Lorsqu'un sommet est lu depuis la mémoire, celui-ci est placé dans ce cache de sommets. Ainsi, lors des utilisations ultérieures, la carte graphique aura juste à lire le sommet depuis ce cache, au lieu de devoir se taper un accès à la mémoire vidéo. Cette mémoire cache étant plus rapide que la mémoire vidéo, les performances augmentent.
Cette mémoire cache ne fonctionne pas sur le même principe que la mémoire vidéo. Il s'agit d'une mémoire cache. Son utilisation est transparente vis à vis de l'assembleur d'entrées. L'assembleur d'entrées ne fait qu'envoyer des adresses mémoires à la mémoire vidéo. Ces accès mémoire sont alors interceptés par la mémoire cache, qui vérifie si cette adresse correspond à une donnée dans le cache de sommets.
Pour cela, chaque sommet est stocké dans la mémoire cache avec son adresse mémoire (ou son indice) : chaque case mémoire stocke à la fois l'adresse et le sommet. Si jamais l'adresse interceptée par le cache est présente dans la mémoire cache, alors le cache renvoie le sommet associé. Sinon, il renvoie l'adresse vers la mémoire vidéo.
Sur les cartes graphiques assez anciennes, cette mémoire cache est souvent très petite : elle contient à peine 30 à 50 sommets, pas plus. Pour profiter le plus possible de ce cache de sommets, les concepteurs de jeux vidéo utilisent diverses optimisations. Il existe diverses techniques permettant de changer l'ordre des sommets en mémoire : avec ces techniques, l'ordre de lecture des sommets depuis la mémoire (géré par les tampons d'indices) est modifié de façon à tenir compte le plus possible du cache. De nombreux travaux scientifiques ont été faits sur le sujet. Les lecteurs intéressés pourront lire une synthèse des différentes techniques en passant par Google.
IV. Transformation▲
Une fois le sommet chargé depuis la mémoire, celui-ci est envoyé dans une unité chargée de le traiter. Celle-ci va effectuer diverses transformations sur chaque sommet qui lui est envoyé.
Notre sommet appartient à un objet, dont la surface est modélisée sous la forme d'un ensemble de points. Chacun de ces points est localisé par rapport au centre de l'objet. Ce centre a, par convention, les coordonnées (0, 0, 0). Les sommets qui forment la surface sont donc repérés par rapport à ce centre.
La première étape à effectuer sur ces sommets consiste simplement à placer cet objet dans la scène 3D. Notre objet sera ainsi placé à un certain endroit dans la scène 3D à afficher. Cet endroit sera repéré par les coordonnées (X, Y, Z). Dans ces conditions, le centre de l'objet passe des coordonnées (0, 0, 0) aux coordonnées (X, Y, Z). Tous les sommets de l'objet doivent être mis à jour.
De plus, notre objet sera placé dans cette scène avec une certaine orientation. Il faut non seulement le placer au bon endroit, mais aussi le faire tourner. Enfin, l'objet peut aussi subir une mise à l'échelle : on peut le gonfler ou le faire rapetisser, du moment que cela ne modifie pas sa forme, mais simplement sa taille. En clair, notre objet subit :
- une translation ;
- une rotation ;
- et une mise à l'échelle.
Ensuite, notre carte graphique va effectuer un dernier changement de coordonnées. Il va passer dans un autre référentiel. Au lieu de considérer un des bords de la scène 3D comme étant le point de coordonnées (0, 0, 0), il va passer dans le référentiel de la caméra. Après cette transformation, le point de coordonnées (0, 0, 0) sera la caméra. La direction de la vue du joueur sera alignée avec l'axe de la profondeur (l'axe Z).
Toutes ces transformations ne sont pas réalisées les unes après les autres. À la place, elles sont toutes effectuées en un seul passage. Pour réussir cet exploit, les concepteurs de cartes graphiques et de jeux vidéos utilisent ce qu'on appelle des matrices. Ces matrices sont des objets mathématiques très utiles dans le rendu 3D. Ce sont de simples tableaux organisés en lignes et en colonnes. Dans chaque case de ces tableaux, on trouve un nombre.
Ces matrices peuvent être définies plus formellement. Plus important, les mathématiciens ont « inventé » ou découvert comment effectuer des calculs avec ces matrices. Il est ainsi possible de prendre un vecteur, et de le multiplier par cette matrice. Le lien avec la 3D, c'est qu'appliquées convenablement sur un ensemble de coordonnées, ces matrices peuvent simuler des translations, des rotations, ou des mises à l'échelle. Pour cela, il suffit de prendre le vecteur qui indique la position d'un sommet par rapport au centre de mon objet : ce vecteur est le vecteur (X, Y, Z), et le multiplier par une matrice qui va bien pour lui faire subir la translation que je veux.
Les matrices qui permettent de simuler ce genre de choses ont toutefois un défaut : ce sont des matrices 4 * 4 : elles ont quatre lignes, et quatre colonnes. Et pour multiplier une matrice par un vecteur, il faut que le nombre de coordonnées dans le vecteur soit égal au nombre de colonnes. Pour résoudre ce petit problème, on ajoute donc une 4e coordonnée à notre vecteur, coordonnée homogène. Pour faire simple, elle ne sert à rien, et est souvent mise à 1, par défaut. Par exemple, si je prends un point de coordonnées (x, y, z, w), la matrice lui faisant faire une translation de vecteur (X, Y, Z) sera celle-ci :
kitxmlcodelatexdvp\begin{bmatrix} 1 & 0 & 0 & X \\ 0 & 1 & 0 & Y \\ 0 & 0 & 1 & Z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}finkitxmlcodelatexdvpUne rotation d'angle thêta autour de l'axe X correspond à cette matrice :
Il existe donc des matrices pour la translation, la mise à l'échelle, d'autres pour la rotation, etc. Et mieux : il existe des matrices dont le résultat correspond à plusieurs opérations simultanées : rotation ET translation, par exemple. Autant vous dire que le gain en termes de performances est assez sympathique.
Ces calculs avec des matrices sont effectués par notre carte graphique. Les anciennes cartes graphiques contenaient un circuit spécialisé dans ce genre de calculs. Ce circuit prenait un sommet, et renvoyait le sommet transformé. Ce genre de circuit était composé d'un gros paquet de multiplicateurs et d'additionneurs flottants. Pour plus d'efficacité, certaines cartes graphiques comportaient plusieurs de ces circuits, afin de pouvoir traiter plusieurs sommets d'un même objet en même temps. De nos jours, ce genre de choses est géré par les processeurs intégrés sur la carte graphique.
V. Éclairage▲
Seconde étape de traitement : l'éclairage. L'éclairage qui est ajouté est assez primitif : les ombres ne sont pas forcément très belles. À la suite de cette étape d'éclairage, chaque sommet se verra attribuer une couleur, qui indiquera son éclairage, sa luminosité. Cette couleur est une couleur codée en RGB. Pour calculer cet éclairage, notre sommet va devoir fournir plusieurs informations : comment ce sommet réagit à la lumière, comment il reflète celle-ci, est-ce que la surface est sombre, etc. Notre sommet va donc fournir ces informations sous la forme de couleurs.
V-A. Données des sommets▲
À partir de ces informations, la carte graphique va devoir calculer quatre couleurs, attribuées à chaque sommet. Chacune de ces couleurs est une couleur au format RGB. Ces quatre couleurs sont :
- la couleur diffuse ;
- la couleur spéculaire ;
- la couleur ambiante ;
- la couleur émissive.
On trouve d'abord la couleur ambiante, qui correspond à la couleur réfléchie par la lumière ambiante. Par lumière ambiante, on parle de la lumière qui n'a pas vraiment de sources de lumière précise. Cette lumière n'est pas émise par une source de lumière, mais englobe la scène 3D et l'éclaire. Elle est égale en tout point de notre scène 3D (d'où le terme lumière ambiante). Elle peut servir pour gérer l'éclairage basique de notre scène 3D. Par exemple, on peut simuler le soleil sans utiliser de sources de lumière grâce à cette couleur.
Sa couleur diffuse vient du fait que la surface d'un objet diffuse une partie de la lumière qui lui arrive dessus dans toutes les directions. Cette lumière « rebondit » sur la surface de l'objet et une partie s'éparpille dans un peu toutes les directions.
Vient ensuite la couleur spéculaire, qui indique la couleur due à la lumière réfléchie par l'objet. Lorsqu'un rayon lumineux touche une surface, une bonne partie de celui-ci est réfléchie suivant un angle bien particulier. Pour ceux qui se souviennent de leurs cours, il s'agit simplement de la réflexion de Snell-Descartes. Suivant l'angle entre la source de lumière, la position de la caméra, son orientation, et la surface, une partie plus ou moins importante de cette lumière réfléchie sera renvoyée vers la caméra. C'est la lumière spéculaire.
Et enfin, on trouve la couleur émissive : c'est la couleur produite par la lumière que produit l'objet. Il arrive que certains objets émettent de la lumière, sans pour autant être des sources de lumières.
Autre paramètre d'une surface : sa brillance. Celle-ci indique si la surface brille beaucoup ou pas.
Notre carte graphique a encore besoin d'un dernier paramètre. Suivant l'angle avec lequel arrive un rayon lumineux sur la surface de l'objet, la réflexion de la lumière ne sera pas la même. Pour gérer l'orientation de la surface, notre sommet est fourni avec une information qui indique comment est orientée la surface : la normale. Cette normale est un simple vecteur, perpendiculaire à la surface de l'objet, dont l'origine est le sommet.

V-B. Calcul de l'éclairage▲
À partir de ces informations, un circuit présent dans notre carte graphique va calculer l'éclairage de notre scène 3D. Il existe plusieurs façons pour éclairer notre scène 3D. Divers algorithmes permettent de calculer la couleur d'un sommet en fonction des paramètres mentionnés plus haut. Les anciennes cartes graphiques, entre la Geforce 256 et la Geforce FX contenaient des circuits câblés capables d'effectuer des calculs d'éclairage simples. Cette fonction de calcul de l'éclairage faisait partie intégrante d'un gros circuit nommé le T&L.
Dans ce qui va suivre, nous allons voir comment notre carte graphique réalisait cet éclairage. Autant prévenir tout de suite, la méthode d'éclairage qui va vous être présentée est une version simplifiée de l'éclairage réellement calculé par le circuit câblé des anciennes cartes graphiques. La méthode présentée dans ce qui va suivre est un simple algorithme d'éclairage de Phong. C'est une amélioration de cette méthode qui est utilisée dans les circuits de T&L. Ce genre d'algorithme donne des résultats d'éclairage assez rudimentaires.
Avec cet algorithme, les quatre couleurs du sommet seront modifiées, avant d'être additionnées toutes ensemble pour produire la couleur finale du sommet : elle sera alors éclairée. Petit détail : vu que nos couleurs sont au format RGB, chaque composante rouge, bleu, ou verte de la couleur sera traitée indépendamment des autres. Ce qui signifie que les calculs qui vont suivre seront appliqués pour chaque composante R, G, ou B de la couleur.
Tout d'abord, la couleur émissive ne change pas : elle ne subit aucun calcul.
Ensuite, la couleur ambiante de notre objet est multipliée par l'intensité de la lumière ambiante.
La couleur diffuse est calculée en multipliant :
- la couleur diffuse du sommet ;
- l'intensité de la source de lumière ;
- et le cosinus entre la normale, et le rayon de lumière qui touche le sommet.
Ce cosinus ne sort pas de nulle part. Il sert à gérer l'orientation de la surface comparée à la source de lumière. Plus le rayon de lumière incident rase la surface de l'objet, moins celui-ci diffusera de lumière. Par contre, plus la lumière arrive droit, plus elle est diffusée.
Ensuite, la lumière réfléchie, spéculaire est calculée. Pour cela, il suffit de multiplier :
- la couleur spéculaire ;
- l'intensité de la source lumineuse ;
- et un paramètre qui dépend de la direction du regard de la caméra, et de la direction du rayon réfléchi par la surface.
Ce rayon réfléchi correspond simplement à la direction qu'aurait un rayon de lumière une fois réfléchi par la surface de notre objet. Pensez à la loi de Snell-Descartes. Le paramètre en question se calcule avec cette formule : cos^brillance (couleur_spéculaire).
Enfin, les quatre couleurs calculées plus haut sont additionnées ensemble.
Comme vous le voyez, ces calculs nécessitent d'effectuer des calculs de cosinus, ainsi que des multiplications et des additions. De plus, ils nécessitent de calculer les vecteurs qui représentent la direction des rayons lumineux émis par la source de lumière, la direction du regard de la caméra, la normale, etc. Notre carte graphique contient donc des circuits pour faire ces calculs. Mais les donner serait hors de portée de ce cours.
Navigation▲
| Tutoriel précédent : Pilotage par le logiciel | Sommaire | Tutoriel suivant : Rasterization |